Carga horária no certificado: 180 horas

Quando a gente vê um gráfico em uma notícia, um relatório de trabalho ou uma planilha no Excel, é comum ficar na dúvida sobre o que aquilo realmente significa.

A primeira coisa que você precisa entender é o que são dados. Dados são basicamente informações organizadas. Por exemplo, a quantidade de vendas de um produto por mês, as notas dos alunos de uma turma ou o número de curtidas em postagens de uma rede social. Esses dados podem ser apresentados de diferentes formas: em tabelas, gráficos, porcentagens, ou até mesmo em frases.

Vamos começar com tabelas. Quando você vê uma tabela, o mais importante é identificar o que está sendo comparado. Os títulos das colunas e das linhas são essenciais. Se você está vendo, por exemplo, uma tabela com os gastos de um projeto mês a mês, observe as colunas: normalmente uma mostra o mês, outra mostra o valor gasto. A primeira dica prática aqui é sempre ler o título da tabela e os rótulos. Eles já dizem muito.

Passando para os gráficos, temos os de barra, de linha e de pizza como os mais comuns. No gráfico de barras, o comprimento da barra representa a quantidade. É muito usado para comparar categorias — por exemplo, número de vendas por produto. Um erro comum é olhar só para a barra maior sem perceber o que ela representa. Sempre leia o eixo X (horizontal) e o eixo Y (vertical).

O gráfico de pizza é aquele em forma de círculo, dividido em fatias. Ele é ótimo para mostrar proporções. Imagine que sua empresa gastou R$ 10.000 no mês e quer mostrar quanto foi para marketing, quanto para salários, e quanto para operação. O gráfico de pizza ajuda a visualizar a proporção de cada gasto dentro do total.

Gráficos de linha, por outro lado, mostram evolução. São ideais para quando você quer ver como algo mudou ao longo do tempo. Por exemplo, se a temperatura de uma cidade está subindo mês a mês, ou se as vendas caíram nos últimos trimestres.

Outro ponto fundamental é entender a média. A média é o valor “central” de um conjunto de dados. Por exemplo, se cinco pessoas ganham R$ 1.000, R$ 1.200, R$ 1.500, R$ 2.000 e R$ 2.300, a média salarial será a soma de tudo dividido por cinco. Mas cuidado: a média pode enganar. Se uma pessoa ganha muito mais que as outras, a média sobe e dá a impressão de que todos ganham mais do que realmente ganham.

Por isso, também é importante conhecer a mediana — que é o valor que fica no meio quando os dados são colocados em ordem. No exemplo acima, a mediana seria R$ 1.500. A mediana é útil especialmente quando há muitos valores muito altos ou muito baixos (os famosos “extremos”, ou “outliers”).

Ainda falando de leitura de dados, preste atenção em porcentagens. Muitas vezes se diz que “o número de acidentes aumentou 50%”. Mas 50% de quê? De 2 para 3 já é um aumento de 50%. Então, sempre que ver uma porcentagem, procure o número original. Isso evita interpretações erradas.

No dia a dia, entender dados significa ser capaz de fazer boas perguntas: “O que essa tabela está comparando?”, “Qual foi o período analisado?”, “Qual a fonte dos dados?”, “Os valores estão absolutos (quantidade) ou relativos (porcentagem)?”, “Há tendência de aumento ou queda?”. Essas perguntas te colocam à frente de muita gente que apenas “olha” um gráfico sem interpretar de verdade.

Por fim, uma habilidade prática fundamental é identificar quando os dados estão sendo usados de forma tendenciosa. Gráficos que começam do meio (ao invés de zero), escalas mal proporcionadas ou ausência de contexto são sinais de que a informação pode estar sendo manipulada para influenciar sua percepção.

 

Então, resumo prático do que vimos até aqui:

• Sempre leia os títulos, rótulos e legendas.

• Gráfico de barra compara, de linha mostra evolução, de pizza mostra proporção.

• Desconfie de médias isoladas: veja também mediana e valores extremos.

• Porcentagens precisam de contexto.

• Faça perguntas: o que, quando, quanto, como e por quê.

 

Com isso, você já terá base para entender e interpretar qualquer gráfico, tabela ou dado que cruzar seu caminho — seja em uma reunião, um relatório, uma matéria de jornal ou uma planilha pessoal.

 

Como eu organizo e resumo qualquer conjunto de dados de forma clara e útil?

No dia a dia, lidamos com dados o tempo todo — sejam números de vendas, avaliações de clientes, respostas de questionários, desempenho de alunos, ou até o controle de gastos pessoais. Mas antes de tirar conclusões, o primeiro passo é organizar esses dados de forma que eles façam sentido. E para isso, existem ferramentas e técnicas simples que qualquer pessoa pode aplicar, mesmo sem experiência com estatística.

Vamos imaginar que você recebeu os resultados de uma pesquisa feita com 50 pessoas sobre o nível de satisfação com um serviço. Os dados vieram todos bagunçados: algumas pessoas deram notas de 1 a 5, outras escreveram comentários, algumas deixaram campos em branco. O primeiro passo é organizar essa bagunça em uma estrutura legível.

A base de tudo é a tabela de dados. Se estiver usando uma planilha como Excel ou Google Sheets, organize as informações em colunas: uma coluna para o nome (ou identificação), uma para a nota dada, outra para o comentário, e assim por diante. Mesmo que os dados sejam simples, esse passo já facilita muito na hora de resumir e analisar.

Agora, com os dados organizados, o próximo passo é resumir a informação, e aqui entram os conceitos de frequência e medidas de tendência central.

A frequência mostra quantas vezes cada valor apareceu. Por exemplo, se você tem 50 avaliações de 1 a 5, talvez descubra que: Nota 1: 5 pessoas | Nota 2: 10 pessoas | Nota 3: 20 pessoas | Nota 4: 10 pessoas | Nota 5: 5 pessoas.

Isso já te dá uma noção clara da distribuição. Ao invés de olhar 50 linhas, você vê rapidamente que a maioria dos clientes deu nota 3.

Com isso, você pode montar uma tabela de frequência, que é a base de qualquer relatório estatístico. Ela pode incluir também a frequência relativa, que mostra os valores em porcentagem (ex: 20 pessoas de 50 = 40%).

A seguir, vamos falar das medidas de tendência central, que são: média, mediana e moda. Essas medidas ajudam a resumir os dados com um único número, facilitando a comunicação e a tomada de decisões.

A média é o valor mais conhecido: soma de todos os valores dividido pelo total de observações. Por exemplo, se os alunos tiraram as notas 5, 6, 7, 8 e 9, a média seria (5+6+7+8+9)/5 = 7. A média é útil quando os dados são equilibrados, mas pode ser enganosa se houver valores extremos. Imagine que quatro pessoas ganham R$ 2.000, e uma ganha R$ 50.000. A média vai subir muito, dando a impressão errada de que todos ganham bem.

Nesses casos, entra a mediana. A mediana é o valor central quando os dados estão em ordem. No exemplo anterior, com salários: R$ 2.000, R$ 2.000, R$ 2.000, R$ 2.000, R$ 50.000 — a mediana é R$ 2.000. Bem mais representativa do que a média. Isso mostra por que a mediana é muito usada em renda, imóveis, tempo de espera, etc.

A moda, por outro lado, é o valor que mais se repete. Em dados categóricos (como marcas preferidas, sabores de pizza, bairros mais citados), a moda é a melhor medida. Se numa pesquisa 100 pessoas disseram qual é seu refrigerante favorito, e 60 disseram Coca-Cola, então a moda é Coca-Cola.

Essas três medidas (média, mediana e moda) são complementares. O ideal é olhar as três para ter uma visão mais completa dos dados. E sempre considerar o contexto.

Agora vamos ver um exemplo prático de organização de dados com gastos mensais. Suponha que você gastou os seguintes valores em alimentação nos últimos 10 dias: R$ 25, R$ 32, R$ 22, R$ 28, R$ 35, R$ 25, R$ 22, R$ 27, R$ 29, R$ 30.

1. Organize em ordem crescente: R$ 22, R$ 22, R$ 25, R$ 25, R$ 27, R$ 28, R$ 29, R$ 30, R$ 32, R$ 35.

2. Média: Soma = 275 | Média = 275 / 10 = R$ 27,50.

3. Mediana: Como temos 10 números, a mediana será a média entre os 5º e 6º valores: (27 + 28)/2 = R$ 27,50.

4. Moda: Os valores 22 e 25 aparecem duas vezes. Temos duas modas.

5. Tabela de frequência: A tabela de frequência apresenta a distribuição de valores observados em um conjunto de dados. Nela, o valor 22 ocorre 2 vezes, assim como o valor 25, que também aparece 2 vezes. Os demais valores — 27, 28, 29, 30, 32 e 35 — aparecem uma única vez cada. Isso indica que, entre os dados registrados, os valores 22 e 25 foram os mais frequentes, enquanto os demais ocorreram com menor frequência. Essa distribuição mostra uma leve concentração em torno desses dois valores, com os demais se espalhando de forma uniforme ao longo do restante do intervalo observado.

 

Com esses dados organizados e resumidos, você consegue responder a perguntas como: Estou gastando muito ou pouco? Meus gastos são consistentes ou muito variados? Quais valores se repetem com mais frequência?

Agora vamos aplicar esse raciocínio em uma empresa. Imagine que você gerencia uma equipe de vendas. Cada vendedor fez um número de vendas no mês: 10, 12, 9, 11, 10, 15, 8, 11, 9, 13.

Você pode:

1. Calcular a média de vendas: (10+12+9+11+10+15+8+11+9+13)/10 = 10,8

2. Ver a mediana (ordem crescente): 8, 9, 9, 10, 10, 11, 11, 12, 13, 15 → mediana = (10 + 11)/2 = 10,5

3. Moda: 9, 10 e 11 aparecem duas vezes cada → múltiplas modas

4. Tabela de frequência: ajuda a ver qual desempenho é mais comum

5. Criar um gráfico de barras simples com os dados organizados: ajuda visualmente a entender os dados e transformá-los em informações.

 

Com isso, você identifica quem está abaixo ou acima da média, se a equipe está equilibrada ou desigual, se há picos de desempenho e muito mais. Tudo isso só com dados simples organizados.

Se você for um professor, pode aplicar a mesma lógica com notas de alunos. Se for um autônomo, pode usar com suas finanças. Se for um empreendedor, pode aplicar em satisfação de clientes. O princípio é o mesmo: organize, resuma e interprete.

 

Então, resumo prático do que vimos até aqui:

• Organize seus dados em colunas e linhas, mesmo que seja no papel.

• Use tabelas de frequência para ver repetições e padrões.

• Calcule média, mediana e moda para resumir o conjunto.

• Analise os dados com atenção a valores extremos.

• Interprete sempre no contexto — o número sozinho não diz tudo.

 

Dominar essa etapa de organização e resumo dos dados te permite partir para análises mais profundas e decisões mais inteligentes — sem depender de ninguém para “explicar” os números pra você.

 

Como eu interpreto gráficos e tabelas para tomar decisões?

Saber interpretar gráficos e tabelas é essencial para qualquer pessoa que lida com dados — seja em uma empresa, no comércio, na escola ou na vida pessoal. Não se trata apenas de “ver o gráfico” ou “olhar a tabela”, mas de entender a história que os dados estão contando. E mais: usar essa história para tomar decisões melhores. Neste módulo, vamos ver como isso funciona na prática, sem enrolação teórica.

Primeiro, é importante entender que todo gráfico é uma tentativa de contar algo de forma visual. Quando alguém mostra um gráfico, ele está tentando te convencer de algo. Por isso, além de entender, você precisa aprender a desconfiar, comparar e cruzar informações.

Vamos começar com o gráfico mais simples e mais usado: o gráfico de colunas (ou barras). Ele é útil para comparar categorias diferentes. Imagine que você é gerente de um restaurante e quer ver qual prato vende mais. Você tem os seguintes dados: Hambúrguer: 120 vendas | Pizza: 80 vendas | Salada: 40 vendas | Macarrão: 60 vendas.

Um gráfico de colunas com esses dados mostra rapidamente qual produto está saindo mais e qual está saindo menos. Você pode ver visualmente a diferença entre eles, e isso ajuda a tomar decisões como: devo tirar a salada do cardápio? Devo investir mais em hambúrgueres? Preciso melhorar o marketing do macarrão?

 

Agora pense no gráfico de pizza (ou setores). Ele mostra a porcentagem de cada categoria dentro do total. É útil quando você quer saber qual parte representa o todo. Usando os mesmos dados de vendas, se você colocar num gráfico de pizza, verá que o hambúrguer representa 40% das vendas totais. Esse tipo de gráfico é bom para mostrar proporções, mas cuidado: ele pode enganar se tiver muitas categorias ou se os valores forem muito parecidos. Às vezes, dois setores parecem do mesmo tamanho, mas têm diferença de 5% que você só percebe olhando os números.

 

Outro gráfico muito comum é o gráfico de linha, excelente para mostrar evolução ao longo do tempo. Digamos que você quer acompanhar suas vendas semanais: Semana 1: R$ 1.000 | Semana 2: R$ 1.200 | Semana 3: R$ 800 | Semana 4: R$ 1.500. Um gráfico de linha vai mostrar os picos e quedas. Assim, você percebe que na terceira semana houve queda nas vendas, o que pode indicar um problema. Se isso se repetir nos meses seguintes, você poderá investigar melhor (foi um feriado? falta de estoque? mudança no comportamento do cliente?).

 

E agora o gráfico de dispersão (ou dispersão de pontos). Ele é ótimo quando queremos ver relação entre duas variáveis. Por exemplo, se você quiser ver se há relação entre tempo de estudo e nota na prova: Estudou 1h → tirou 5 | Estudou 2h → tirou 6 | Estudou 3h → tirou 8 | Estudou 4h → tirou 9 | Estudou 5h → tirou 10. Colocando isso num gráfico de dispersão, verá uma tendência crescente. Isso mostra que quanto mais se estuda, maior tende a ser a nota. Claro, nem toda relação é direta, mas esse gráfico serve para enxergar padrões invisíveis quando olhamos só os números. Muito usado em ciência, finanças e gestão de desempenho.

 

Agora vamos falar das tabelas. Muita gente ignora, mas a tabela é o começo de tudo. Sem uma boa tabela, não existe gráfico confiável. É nela que os dados são organizados de forma detalhada. Por isso, ao receber uma tabela, sua primeira atitude deve ser:

1. Verificar o que está nas colunas e nas linhas.
2. Checar as unidades (R$, %, unidades, km, etc).
3. Observar totais, médias, e outliers (valores muito fora da curva).
4. Fazer comparações simples entre linhas e colunas.

 

Vamos imaginar uma tabela de desempenho de vendedores:

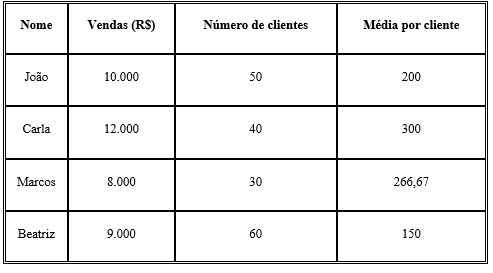
Olhando apenas a coluna “Vendas”, Carla parece ser a melhor. Mas quando você olha a “Média por cliente”, percebe que ela de fato é mais eficiente — vende mais para menos pessoas. Por outro lado, Beatriz atendeu mais clientes, mas vendeu menos por pessoa. Isso é essencial para tomar decisões estratégicas: quem merece bônus? Quem precisa de treinamento? Quem tem potencial para liderar?

Outro ponto importante é aprender a interpretar a intenção por trás dos dados. Às vezes, uma empresa mostra um gráfico dizendo “crescemos 200% em um mês!”, mas não mostra que o valor anterior era de apenas R$ 100 e subiu para R$ 300. O crescimento percentual é alto, mas o impacto real é pequeno. Então, sempre que ver porcentagem, pergunte: “em cima de quê?”.

Além disso, gráficos mal construídos ou distorcidos podem te enganar. Cuidado com:

1. Eixos cortados: quando o eixo Y (vertical) não começa do zero, uma pequena diferença pode parecer enorme.

2. Escalas diferentes: dois gráficos comparando variáveis diferentes, mas com escalas que favorecem uma interpretação equivocada.

3. Cores chamativas ou exageradas: muitas vezes usadas para manipular a atenção de quem vê.

 

Agora vamos trazer isso para um exemplo da vida real. Você trabalha em uma escola e recebe um relatório com o seguinte gráfico:

 

Gráfico de colunas – Notas médias por disciplina: Português: 6,5 | Matemática: 5,2 | História: 7,1 | Ciências: 4,9 | Inglês: 6,0.

 

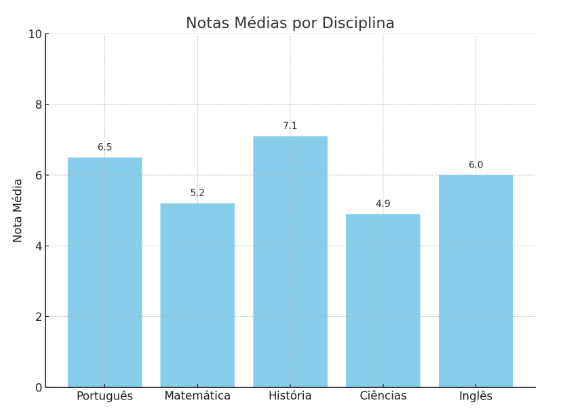
Ao ver esse gráfico acima, você percebe que Ciências está com a menor média. O que fazer com essa informação? Você pode decidir:

1. Conversar com os professores para entender a dificuldade.

2. Aplicar um reforço escolar nessa disciplina.

3. Cruzar esses dados com outros (como taxa de faltas ou histórico das turmas) para entender melhor.

 

A chave aqui é: o gráfico sozinho não responde nada, ele só aponta para onde você deve olhar.

 

Outro exemplo: imagine que você trabalha com marketing digital e recebe este gráfico de linha:

Gráfico – Cliques em anúncios nos últimos 7 dias: Segunda: 150 | Terça: 300 | Quarta: 500 | Quinta: 700 | Sexta: 600 | Sábado: 400 | Domingo: 200.

 

Esse gráfico mostra claramente que quinta-feira é o dia com mais cliques. Logo, talvez seja interessante investir mais em anúncios nesse dia, aumentar o orçamento ou planejar campanhas especiais para essa data.

 

Resumo prático do que aprendemos agora:

• Gráfico de colunas: comparar categorias.

• Gráfico de pizza: mostrar proporções.

• Gráfico de linha: acompanhar evolução no tempo.

• Gráfico de dispersão: ver relação entre variáveis.

• Tabelas: base para análise completa e confiável.

• Sempre cheque unidades, proporções, e contextos antes de tirar conclusões.

• Cuidado com distorções visuais e manipulações intencionais.

 

Dominar a leitura de gráficos e tabelas te dá autonomia para interpretar relatórios, questionar informações e decidir com mais confiança. Você deixa de ser só um espectador dos dados e passa a ser um analista prático, mesmo sem precisar de fórmulas ou softwares avançados.

 

Como eu uso médias, medianas e modas para tomar decisões no cotidiano?

Na prática, quase todos os dias somos expostos a médias, medianas e modas — e muitas vezes não percebemos isso. Quando alguém diz “a média salarial no Brasil é X” ou “a média de notas da turma foi Y”, está usando estatística descritiva. Mas será que você entende mesmo o que isso significa? E mais importante: sabe quando confiar nesses números, e quando não confiar? É isso que vamos ver agora, com foco total na aplicação prática.

Vamos começar com o mais conhecido: a média. Também chamada de média aritmética, é o valor que se obtém somando todos os dados e dividindo pelo número de elementos. Simples. Por exemplo, se você ganhou R$ 1.000 em janeiro, R$ 1.500 em fevereiro e R$ 2.000 em março, a média do trimestre foi: (1000 + 1500 + 2000) / 3 = R$ 1.500.

Mas atenção: a média pode enganar quando há valores extremos (outliers). Imagine que numa empresa 9 funcionários ganham R$ 2.000 e o dono ganha R$ 100.000. A média salarial será: [(9 × 2000) + 100000] / 10 = (18000 + 100000) / 10 = R$ 11.800

Parece que todos ganham bem, né? Mas isso não reflete a realidade da maioria. Por isso, em muitos contextos, a mediana é mais adequada.

A mediana é o valor central de um conjunto de dados ordenado. Se há número ímpar de valores, é o do meio. Se for par, é a média dos dois centrais. Vamos ver um exemplo:

• Salários: R$ 1.200, R$ 1.500, R$ 1.800, R$ 2.000, R$ 2.500Mediana = R$ 1.800 (o terceiro valor da sequência ordenada)

• Agora, adicionando o salário de um executivo de R$ 100.000: R$ 1.200, R$ 1.500, R$ 1.800, R$ 2.000, R$ 2.500, R$ 100.000

• Mediana = (R$ 1.800 + R$ 2.000) / 2 = R$ 1.900

 

Percebeu? A mediana resiste melhor a valores extremos e mostra de forma mais realista como a maioria vive.

A moda, por outro lado, é o valor que mais se repete. Pode haver mais de uma moda (bimodal, trimodal) ou nenhuma (se todos os valores forem únicos). Ela é útil para entender preferências ou tendências de consumo.

Imagine que você é dono de uma loja e vende camisetas nos tamanhos P, M, G e GG. Se os tamanhos vendidos em uma semana forem: M, M, G, M, P, G, GG, M, P, M. Moda = M (foi o mais vendido, aparece 5 vezes). Essa informação ajuda no reabastecimento de estoque, mostrando qual tamanho deve ser priorizado. É simples e extremamente útil.

Agora vamos para a interpretação e uso no dia a dia. Suponha que você é responsável pela análise de desempenho dos vendedores de uma loja. Os vendedores fizeram as seguintes quantidades de vendas no mês: João: 20 | Carla: 22 | Pedro: 25 | Júlia: 100 | Ana: 21. A média é: (20 + 22 + 25 + 100 + 21) / 5 = 188 / 5 = 37,6 vendas.

Se você usasse essa média para comparar todos, pareceria que João, Carla, Pedro e Ana foram mal. Mas, na verdade, foi a Júlia que teve um desempenho excepcional, enquanto os outros tiveram resultados parecidos. A mediana (ordenando: 20, 21, 22, 25, 100) é 22, que representa melhor a “média” real do grupo. A moda aqui não existe, pois não há repetição, mas se houvesse vários vendedores com 20 vendas, por exemplo, isso indicaria uma tendência.

Outro exemplo prático: imagine que você é professor e aplicou uma prova. As notas foram: 5, 6, 6, 7, 7, 7, 8, 9, 10, 10.

1. Média = (5 + 6 + 6 + 7 + 7 + 7 + 8 + 9 + 10 + 10) / 10 = 75 / 10 = 7,5

2. Mediana = (7 + 7) / 2 = 7

3. Moda = 7 (apareceu 3 vezes)

 

Aqui, a moda e a mediana estão mais próximas da realidade da turma do que a média. Se a prova foi muito difícil, mas alguns alunos foram bem acima da média, eles puxaram o valor para cima.

Você também pode usar esses conceitos em decisões financeiras pessoais. Vamos supor que você quer saber quanto gasta por semana em alimentação fora de casa. Nos últimos 5 dias: Segunda: R$ 15 | Terça: R$ 18 | Quarta: R$ 100 | Quinta: R$ 20 | Sexta: R$ 22. A média é R$ 35. Mas esse valor não representa seu gasto normal — só está alto por causa de um almoço especial na quarta. A mediana, nesse caso, é R$ 20, que reflete melhor sua rotina. Essa análise pode te ajudar a planejar melhor seus gastos reais.

Mais um uso prático: em uma pesquisa de mercado, você coleta a opinião de 100 pessoas sobre o tempo de espera em um atendimento. Os tempos variam de 1 a 120 minutos. A média dá 45 minutos, mas a mediana é 30. Isso mostra que a maioria das pessoas espera menos do que 45 minutos — ou seja, os piores casos estão distorcendo a média. A mediana, nesse caso, deve ser usada para definir metas realistas de melhoria.

Um erro muito comum é usar média quando o conjunto é desigual. Por exemplo, avaliar a qualidade de escolas públicas pela média do IDEB pode ser injusto, pois escolas de regiões muito carentes podem ter nota extremamente baixa e puxar o valor geral para baixo, mesmo que a maioria esteja na média. A mediana poderia ser mais justa nesse cenário.

Agora um exemplo do mundo corporativo. Suponha que você gerencie um time de vendas e precisa decidir quem receberá um bônus por desempenho. As vendas no trimestre foram: Vendedor A: R$ 5.000 | Vendedor B: R$ 5.500 | Vendedor C: R$ 6.000 | Vendedor D: R$ 30.000 | Vendedor E: R$ 4.000. A média é R$ 10.100, que só o Vendedor D superou. Isso seria justo? Talvez não. A mediana é R$ 5.500 — o que indica que o desempenho típico está nesse patamar. Você pode definir bônus com base em quem superou a mediana, e não a média, para que o prêmio seja mais realista.

A moda também ajuda no setor de serviços. Imagine que você é dono de uma pizzaria e analisou os sabores pedidos durante um mês. Se calabresa aparece 300 vezes, frango 150, marguerita 120 e quatro queijos 280, a moda é calabresa. Você pode: Criar promoções focadas nesse sabor, comprar mais ingredientes com desconto e/ou criar variações ou combos com ele.

Resumindo, os três conceitos funcionam melhor quando usados juntos. Nenhum deles é “melhor” por si só. Tudo depende do objetivo da análise e do contexto. Para facilitar:

1. Use a média quando os dados forem equilibrados e sem extremos.

2. Use a mediana quando houver valores muito diferentes ou fora da curva.

3. Use a moda para identificar preferências, comportamentos mais frequentes ou padrões.

 

Dica bônus: se você for usar esses valores para apresentar relatórios, deixe claro qual deles está usando. Diga “a média salarial é R$ 2.500, mas a mediana é R$ 1.900” — isso mostra mais transparência e inteligência analítica.

Dominar o uso de média, mediana e moda te ajuda a tomar decisões mais inteligentes, a apresentar dados com mais clareza e a evitar ser enganado por números que parecem bons, mas não contam a história inteira. Não é exagero dizer que essas três ferramentas simples podem transformar sua forma de ver o mundo.

 

Como eu interpreto gráficos e tabelas para entender dados no dia a dia?

Vivemos em uma era em que tudo é medido e exibido em gráficos: desde o desempenho da bateria do celular até os resultados de uma pesquisa eleitoral ou os dados de um treino na academia. E interpretar esses gráficos e tabelas corretamente é fundamental para não ser enganado, tomar boas decisões e comunicar ideias com clareza. Neste módulo, você vai aprender, de forma 100% prática, a entender e usar gráficos e tabelas com confiança no dia a dia.

Vamos começar com os tipos mais comuns de gráficos, e que já abordamos anteriormente:

1. Gráfico de colunas: usado para comparar quantidades. Muito comum em relatórios de vendas, desempenho mensal, produção de fábricas, etc. Imagine que você tem uma planilha com as vendas semanais de uma loja de roupas: Semana 1: R$ 1.200 | Semana 2: R$ 1.500 | Semana 3: R$ 900 | Semana 4: R$ 2.000. Se você colocar isso em um gráfico de colunas, fica imediatamente visível qual semana teve melhor desempenho. Sem precisar de cálculos, o olho capta o tamanho da coluna e entende o dado.

2. Gráfico de linhas: ótimo para mostrar evolução ao longo do tempo. Por exemplo: a evolução do peso de alguém que está fazendo dieta. Se a linha desce, significa perda de peso. Se sobe, ganho. Você pode usar esse tipo de gráfico para ver tendências em qualquer área: engajamento nas redes sociais, nota média de alunos, crescimento de lucros, entre outros.

3. Gráfico de pizza (ou setores): usado para mostrar proporções de um total. Suponha que você analisou o tempo que passa em frente à tela do celular em um dia: Redes sociais: 3 horas | Vídeos: 2 horas | Jogos: 1 hora | Mensagens: 2 horas | Outros: 2 horas. Total: 10 horas. Um gráfico de pizza mostra cada categoria como uma “fatia”, permitindo perceber, por exemplo, que 30% do seu tempo foi em redes sociais. É uma ótima ferramenta para autoconhecimento e ajustes de rotina.

4. Tabelas: são formas organizadas de apresentar dados em colunas e linhas. Elas não têm o apelo visual dos gráficos, mas são extremamente úteis quando precisamos de precisão nos valores. Imagine que você tem os dados de temperatura de cada dia de um mês. Um gráfico mostra a tendência, mas só a tabela vai te permitir saber exatamente quantos graus fez no dia 14, por exemplo.

 

Agora que você conhece os principais formatos, vamos ao que realmente importa: como interpretar isso no dia a dia.

Suponha que você veja uma manchete assim: “Gráfico mostra que o número de casos de gripe caiu 40% em abril”. Você olha o gráfico e vê uma linha caindo. Mas ao analisar a tabela ao lado, descobre que: Março: 10 casos | Abril: 6 casos. A linha caiu, de fato. Mas será que 4 casos a menos é uma queda tão significativa assim? Depende. Se forem só 10 pessoas ao todo, a queda é pequena. Se forem milhares, é relevante. Por isso, nunca analise um gráfico isolado sem verificar os dados que o sustentam.

Outro ponto crítico: escala do gráfico. Uma manipulação comum é alterar a escala para forçar a percepção de crescimento ou queda. Imagine este exemplo: Gráfico A – Vendas de janeiro a março: Janeiro: R$ 1.000 | Fevereiro: R$ 1.100 | Março: R$ 1.200. Se a escala do gráfico for de 0 a 1.500, a linha vai parecer suave. Mas se a escala for de 1.000 a 1.250, a linha vai parecer uma subida gigante, criando a impressão de um crescimento agressivo. O dado é o mesmo, mas a percepção muda conforme a escala.

Outro cuidado essencial: contexto. Veja esse exemplo: “Empresa X cresceu 80% em faturamento!” Uau! Impressionante, né? Mas se você olhar a tabela: Faturamento em 2023: R$ 10 mil | Faturamento em 2024: R$ 18 mil. Cresceu, sim. Mas o valor ainda é pequeno. Às vezes os percentuais enganam. Sempre compare o número absoluto também. O ideal é sempre se perguntar: “80% de quanto?”.

Vamos falar agora sobre como usar gráficos no seu cotidiano. Suponha que você está montando uma planilha para acompanhar seus gastos mensais. Você registra: Aluguel | Alimentação | Transporte | Lazer | Emergências. Ao gerar um gráfico de pizza, você vê que 60% da sua renda vai para aluguel e alimentação. Isso te permite enxergar onde está gastando mais e pensar em estratégias para equilibrar melhor as despesas. Gráficos são ótimos para tomar decisões com base visual — o que facilita muito.

Você também pode usar gráficos para acompanhar metas. Exemplo: você quer perder 5kg em dois meses. Você mede seu peso toda semana e gera um gráfico de linha. A visualização dessa linha caindo (ou subindo, se você estiver falhando) te dá um retorno instantâneo de como está seu desempenho. Isso vale também para finanças, estudos, produtividade, etc.

E quando você precisa apresentar dados para outras pessoas? Digamos que você esteja explicando a um cliente por que o faturamento caiu. Você pode dizer: “Nos últimos 3 meses, tivemos uma queda de 15%.” Mas se você mostrar um gráfico de linha com os valores reais e marcar as datas de feriados, reformas ou baixa no estoque, a mensagem fica mais clara e convincente.

 

Aqui vão dicas práticas para interpretar qualquer gráfico com segurança:

1. Olhe o título: ele deve dizer claramente o que o gráfico representa.

2. Verifique a fonte: de onde vêm os dados? São confiáveis?

3. Leia os eixos (no caso de gráficos de linha ou colunas): entenda o que cada eixo representa.

4. Observe a escala: uma escala distorcida muda a percepção.

5. Procure tendências: está subindo? Descendo? Oscilando?

6. Compare com outros dados: se possível, veja outros gráficos, ou a tabela original.

7. Desconfie de gráficos sem valores exatos: às vezes eles omitem números para te manipular.

 

E quando você for criar seus próprios gráficos? Aqui vão boas práticas:

1. Use cores contrastantes, mas evite exageros (cores demais confundem).

2. Sempre coloque legendas claras.

3. Use gráficos diferentes para objetivos diferentes: pizza para proporções, linha para evolução, colunas para comparação direta.

4. Nunca esconda dados importantes. A transparência gera confiança.

5. Evite “embelezamentos” que atrapalham a leitura, como sombras, 3D e enfeites inúteis.

 

Por fim, vale lembrar: um gráfico bem feito pode explicar em 5 segundos o que um texto de 2 páginas levaria minutos. E ao mesmo tempo, um gráfico mal feito pode enganar, esconder ou distorcer a verdade. Por isso, você precisa saber tanto ler quanto criar gráficos e tabelas com inteligência. Saber interpretar gráficos e tabelas é uma habilidade valiosa para qualquer área: negócios, estudos, saúde, comunicação, política e até vida pessoal. Com esse módulo, você aprendeu a fazer isso com visão crítica, prática e estratégica.

 

Como eu aplico a estatística para resolver problemas reais no meu trabalho, estudos ou vida pessoal?

Aplicar estatística no dia a dia é como ter uma lente de aumento para enxergar padrões que normalmente passariam despercebidos. Não se trata apenas de fórmulas ou gráficos bonitos, mas de transformar números em decisões mais inteligentes. A seguir, veja como a estatística pode ser aplicada, de forma prática e acessível, no trabalho, nos estudos, na vida pessoal e até nas finanças e saúde.

 

No trabalho: decisões baseadas em dados reais

Imagine que você é gestor de um restaurante e precisa entender por que as vendas caíram nas últimas semanas. Ao registrar o número de clientes por dia e o ticket médio de consumo, você nota que o movimento caiu principalmente às quartas-feiras, após a suspensão de uma promoção “rodízio em dobro”. Com essa evidência, decide reativar a oferta e os números voltam a crescer. Aqui, o que parece um simples “palpite” vira uma ação embasada em dados.

Outro exemplo: em uma empresa de logística, você analisa os tempos de entrega por região. Calculando a média e o desvio padrão, percebe que os atrasos estão concentrados em uma rota específica. Ao investigar, identifica um gargalo na triagem. A partir disso, reorganiza as equipes e reduz o tempo de entrega em 15%. Sem a estatística, talvez isso passasse despercebido.

 

Na educação: aprendizado com foco em desempenho

Se você é professor, pode usar estatística para entender como suas turmas evoluem. Após aplicar duas provas no semestre, calcula a média e nota que, apesar de a média ter subido, o desvio padrão aumentou — ou seja, alguns alunos foram muito bem, outros muito mal. Isso sugere desigualdade de aprendizado. A solução? Reforço direcionado para quem teve pior desempenho.

Para estudantes, estatística é uma aliada poderosa na hora de se preparar para exames. Suponha que você estude para um vestibular e registre quantas questões erra por tema. Descobre que 70% dos seus erros estão concentrados em geometria e interpretação de gráficos. Com isso, reorganiza sua rotina e foca nesses pontos fracos. É um plano de estudos guiado por dados — e não só por “achismo”.

 

Na vida pessoal: mudar hábitos de forma consciente

Vamos supor que você quer melhorar sua alimentação. Você registra tudo o que come por duas semanas, categoriza os alimentos e percebe que consome fritura cinco vezes por semana, enquanto vegetais aparecem só em três refeições. Ao transformar hábitos em números, você consegue visualizar padrões e estabelecer metas reais — por exemplo, reduzir a fritura para duas vezes por semana e aumentar vegetais para todos os almoços.

Quer um exemplo ainda mais cotidiano? Você percebe que sempre chega atrasado ao trabalho. Ao registrar o tempo gasto no trajeto por um mês, nota que quando sai até 7h15, leva em média 32 minutos. Quando sai depois disso, o tempo médio salta para 48 minutos. A solução está clara: sair mais cedo. Essa pequena análise pode mudar sua rotina e reduzir estresse diário.

 

Finanças pessoais: clareza sobre gastos e metas

Muita gente só percebe que está gastando demais quando já entrou no vermelho. Usar estatística ajuda a evitar esse tipo de surpresa. Imagine que você anota seus gastos por categoria e monta um gráfico: percebe que 40% do seu dinheiro está indo para delivery e cafés na rua. Você define uma meta de gastar no máximo 20% com isso e passa a cozinhar mais em casa.

Ou ainda: você quer planejar quanto economizar para uma viagem. Analisa seus últimos 6 meses e vê que conseguiu poupar, em média, R$ 350 por mês. Com isso, projeta que em 10 meses terá R$ 3.500. A média vira uma ferramenta de planejamento realista.

 

Saúde e esporte: medir progresso com precisão

Se você pratica atividade física, sabe como é fácil se desmotivar. Mas ao registrar seu progresso — tempo de corrida, distância, frequência semanal — você enxerga sua evolução. Por exemplo: no primeiro mês, corre 3 km em 24 minutos; no terceiro, faz 5 km em 27. Você percebe não só que está correndo mais, mas que seu ritmo melhorou. E mais: usando o desvio padrão, identifica se está tendo constância ou se está muito irregular, o que pode indicar cansaço ou overtraining.

O mesmo vale para sono, peso, ingestão de água, pressão arterial, entre outros. Registrar dados da sua rotina permite fazer ajustes informados e acompanhar os resultados com clareza.

 

Evitando erros de interpretação: a estatística exige contexto

Importante lembrar que estatística não é mágica — ela exige cuidado. Por exemplo, se um restaurante diz que “90% dos clientes recomendam”, mas só 10 pessoas responderam, esse dado tem pouco valor. Ou ainda: usar média salarial de um grupo com muitos extremos distorce a realidade — uma pessoa com renda altíssima pode inflar os números.

Sempre se pergunte:

1. Quem coletou os dados?

2. Quantas pessoas participaram?

3. Os dados são confiáveis e bem distribuídos?

4. Existe algum viés escondido?

 

Resumo prático: como aplicar estatística na sua rotina

• Colete dados simples e consistentes. Use cadernos, planilhas, apps. Registre tempo, gasto, quantidade, desempenho, humor — o que for relevante para o seu objetivo.

• Organize visualmente. Gráficos, tabelas, médias e frequências ajudam a dar sentido aos números.

• Observe padrões. Identifique picos, quedas, repetições e desvios.

• Tome decisões com base nesses padrões. Ajuste hábitos, redirecione esforços, otimize tempo.

• Monitore de novo. A estatística é cíclica: colete, analise, aja e reavalie.

 

Em resumo, estatística é como um GPS para decisões. Ajuda a sair do “achismo”, guia suas escolhas com base em fatos e oferece um caminho mais claro rumo a objetivos concretos — seja no trabalho, nos estudos, na saúde ou na vida cotidiana.

 

Como eu apresento os resultados estatísticos de forma clara e convincente para outras pessoas?

Apresentar resultados estatísticos de forma clara e convincente é mais do que mostrar números: é transformar dados em decisões. Você pode até ter feito uma análise brilhante, com gráficos sofisticados e cálculos complexos, mas se ninguém entender o que aquilo significa, o valor do seu trabalho desaparece. Comunicação estatística é, essencialmente, uma tradução — dos números para a linguagem do cotidiano, das evidências para as ações práticas. E, como toda boa tradução, ela exige sensibilidade, clareza e empatia com quem vai receber a mensagem.

Imagine que você está em uma reunião com a diretoria da empresa onde trabalha. Você analisou as vendas dos últimos meses e percebeu uma queda de 12%. Apontar esse número, isolado, pode gerar reações variadas — preocupação, confusão, ou até desinteresse. Agora, se você disser: “As vendas caíram 12% desde janeiro, principalmente nas quartas-feiras, quando pausamos as campanhas de mídia paga. Isso sugere que a retomada dos anúncios nesse dia pode recuperar parte das perdas”, a conversa muda. Você não só apresentou o dado, como explicou o contexto e ofereceu uma solução. O dado virou argumento, e o argumento virou direção.

Esse é o verdadeiro papel de uma apresentação com dados estatísticos: provocar entendimento e, a partir dele, ação. Para isso, a comunicação precisa ser construída com propósito. Antes de qualquer coisa, é importante ter clareza sobre o que você quer que o público compreenda. Você quer que aprovem um orçamento? Que mudem um processo? Que priorizem uma tarefa? Essa resposta vai guiar sua escolha de dados, sua narrativa e a forma como vai estruturar sua apresentação.

A seleção dos dados é outro ponto essencial. Menos é mais. Uma apresentação eficiente traz os números que sustentam sua mensagem principal — e não um mar de estatísticas que confundem em vez de convencer. Suponha que você esteja defendendo a contratação de mais um atendente no call center. Você pode mostrar que o tempo médio de espera dos clientes subiu de 1m40s para 3m15s nos últimos dois meses. Em seguida, mostre que o número de atendimentos por pessoa aumentou 22%. Por fim, conecte os dados com o impacto: “Nosso índice de satisfação caiu de 8,9 para 6,5. Clientes estão desistindo da ligação, e isso está nos custando, em média, 14 pedidos perdidos por semana.” Essa é uma cadeia de raciocínio poderosa: dado → impacto → necessidade → decisão.

Gráficos são grandes aliados — quando bem utilizados. Um gráfico deve, acima de tudo, facilitar o entendimento. Use tipos visuais que combinem com o tipo de informação que você quer mostrar: gráficos de linha para evolução ao longo do tempo, colunas para comparações diretas, pizza para proporções. E nunca subestime a importância da escala: começar um gráfico de barras no número 500, em vez de zero, pode inflar visualmente diferenças pequenas e gerar conclusões distorcidas. Um exemplo cotidiano disso está na apresentação de contas de luz em condomínios: se alguém monta um gráfico com escalas inadequadas para mostrar que o gasto com elevadores “explodiu” de um mês para o outro, pode criar uma sensação falsa de crise, quando na verdade o aumento foi de R$ 80.

Nos relatórios escritos, a lógica deve prevalecer sobre a estética. Comece sempre com um objetivo bem definido — algo como “Analisar a frequência de faltas dos alunos no primeiro trimestre”. Explique rapidamente sua metodologia, como os dados foram coletados, quais períodos ou grupos foram analisados. A seguir, apresente os resultados com clareza, destacando padrões e anomalias, mas sempre com uma linguagem acessível. Em vez de escrever “houve uma dispersão elevada nas turmas noturnas”, prefira: “As turmas da noite tiveram grandes variações de presença — algumas com excelente frequência, outras com altos índices de ausência.” Isso aproxima a estatística da realidade vivida.

Um cuidado essencial é adaptar a linguagem ao público. Se você está falando com alguém sem formação estatística, evite jargões técnicos. Em vez de dizer “o desvio padrão foi elevado”, diga “os resultados variaram bastante entre as pessoas”. Transforme porcentagens em visualizações mentais: “25% dos funcionários faltaram ao menos uma vez no mês” pode virar “a cada quatro pessoas, uma não compareceu em pelo menos um dia”. Use metáforas e comparações: “Nosso índice de satisfação caiu de 4,8 para 4,2 — como se uma prova com nota 9 agora estivesse com nota 8,4”.

E nunca perca de vista o fim dessa comunicação: a tomada de decisão. Cada dado precisa apontar para alguma coisa. Uma forma prática de construir esse raciocínio é usar uma sequência lógica em três partes. Primeiro, apresente o fato: “Em abril, o número de novos usuários caiu 30%.” Depois, explique o significado: “Isso reduziu em R$ 5.200 a receita esperada para o mês.” Por fim, aponte o que pode ser feito: “Precisamos rever a campanha de captação e entender se o público-alvo mudou.”

Com o tempo, você vai desenvolver sua própria forma de comunicar estatística — com seu vocabulário, suas metáforas preferidas, seu jeito de montar gráficos e slides. Mas três princípios nunca mudam: clareza, relevância e narrativa. Clareza para ser entendido sem esforço. Relevância para mostrar só o que importa. Narrativa para guiar a audiência do problema até a solução. Com isso, você transforma dados em decisões — e a estatística deixa de ser apenas um cálculo para se tornar uma ferramenta real de transformação no seu trabalho, nos seus estudos e na sua vida.